A intensidade de cada interação é definida pela sua constante de acoplamento, um parâmetro adimensional que serve para comparar as diferentes interações. No caso particular da interação eletromagnética, a constante de acoplamento é obtida a partir da expressão da energia potencial eletrostática entre duas cargas puntiformes divida pelor fator ħc.
equação Graceli estatística tensorial quântica de campos 1 / / / G G [DR] = .= + G* = = [ ] ω , , / T] / c [ [x,t] ] = |
//////
A constante de acoplamento da interação eletromagnética é também conhecida como a constante de estrutura fina , já substituindo os valores das constantes. Na tabela a seguir são apresentadas características específicas de cada interação:[
Na física, a mecânica quântica relativista (RQM) é qualquer formulação covariante de Poincaré de mecânica quântica. Esta teoria é aplicável a partículas massivas[1] que se propagam em todas as velocidades até as comparáveis à velocidade da luz c e podem acomodar partículas sem massa.[2][3] A teoria tem aplicação em física de alta energia,[4] física de partículas e física de aceleradores,[5][6] bem como física atômica, química[7] e física da matéria condensada.[8][9]
Operador de velocidade
O operador de velocidade Schrödinger/Pauli pode ser definido para uma partícula maciça usando a definição clássica p = m v, e substituindo os operadores quânticos da maneira usual:[10]
equação Graceli estatística tensorial quântica de campos 1 / / / G G [DR] = .= + G* = = [ ] ω , , / T] / c [ [x,t] ] = |
//////
que possui autovalores que possuem qualquer valor. Na RQM, a teoria de Dirac, é:
equação Graceli estatística tensorial quântica de campos 1 / / / G G [DR] = .= + G* = = [ ] ω , , / T] / c [ [x,t] ] = |
//////
que deve ter autovalores entre ± c. Mais antecedentes teóricos podem ser visto na transformação de Foldy-Wouthuysen.[11][12][13][14]
Na mecânica quântica, a paridade intrínseca é um fator de fase que surge como um autovalor de paridade de operação (uma reflexão sobre a origem). Para ver de que a paridade do autovalores são fase de fatores, assumimos um estado puro da paridade de operação (isto é realizado porque o paridade intrínseca é uma propriedade de uma espécie da partícula) e usar o fato de que duas transformações de paridades deixam as partículas no mesmo estado, assim, a nova função de onda pode diferir apenas por um fator de fase, por exemplo: assim, >, já que estas são apenas estados puros satisfazem a equação acima.
A fase de paridade intrínseca é conservada para as interações não-fracas (o produto das paridades intrínsecas é o mesmo antes e depois da reação). Como o Hamiltoniano é invariante sob uma transformação de paridade. A intrínseca a paridade de um sistema é o produto da intrínseca paridades das partículas, por exemplo, para partículas não-interagentes, temos . Desde que a paridade comuta com o Hamiltoniano
equação Graceli estatística tensorial quântica de campos 1 / / / G G [DR] = .= + G* = = [ ] ω , , / T] / c [ [x,t] ] = |
//////
e seu autovalor não se altera com o tempo, portanto, as fases da paridades intrínsecas é uma quantidade conservada.
Uma consequência da equação de Dirac é que a paridade intrínseca de fermions e os antifermiones obedecem a relação e , portanto, as partículas e suas antipartículas, o contrário de paridade. Únicos léptons jamais podem ser criados ou destruídos em experiências, como o número leptônico é uma quantidade conservada. Isso significa que os experimentos são incapazes de distinguir o sinal de uma paridade de léptons, de modo que, por convenção, é escolhido que léptons tem paridade intrínseca de +1, antileptons tem . Da mesma forma, a paridade dos quarks é escolhido ser o +1, e antiquarks é -1.[1]
Para um sistema físico composto por partículas de spin zero, existe um potencial de Coulomb blindado que é conhecido como potencial de Yukawa. Tal pontencial é da forma
equação Graceli estatística tensorial quântica de campos 1 / / / G G [DR] = .= + G* = = [ ] ω , , / T] / c [ [x,t] ] = |
//////
e que é, claramente, um potencial do tipo central. Na equação acima, é uma constante (positiva) de acoplamento que configura a intensidade da força efetiva, é a massa da partícula afetada pelo potencial, é a velocidade da luz e a constante de Planck. Naturalmente, podemos mostrar que o potencial está associada a uma força sempre atrativa.
A História
Hideki Yukawa (físico teórico japonês) mostrou na década de 1930 que tal potencial resulta da interação/troca de um campo escalar massivo como o campo de um bóson, também maciço. Uma vez que o mediador do campo correspondente tem um certo alcance, que é inversamente proporcional à massa do mediador de partícula [1]. Dado que o alcance aproximado da força nuclear era conhecido, a equação Yukawa poderia ser utilizada para prever o massa de repouso aproximada da partícula mediadora do campo de força, mesmo antes de ser descoberto. No caso da força nuclear, esta massa foi previsto ser cerca de 200 vezes a massa do elétron, e isto foi mais tarde considerado ser uma previsão da existência do píon, antes de ter sido detectado, em 1947.
Tal potencial tem várias aplicações, incluindo a interacção entre dois núcleos. Dois núcleos podem experimentar forte interação atrativa devido à taxa de câmbio pions carregados, semelhante à forma como duas partículas interagem eletromagneticamente através da troca de fótons. Como o campo eletromagnético é "transportado" por fótons, o campo piônico potencial, expressamente descrito por Yukawa, é "transportado" por pions.
Relação com o potencial de Coulomb
Se tomarmos o limite → (ou até mesmo a igualdade) no potencial de Yukawa, nós temos
equação Graceli estatística tensorial quântica de campos 1 / / / G G [DR] = .= + G* = = [ ] ω , , / T] / c [ [x,t] ] = |
//////
de modo que podemos identificar a equação acima, com a ε, como o potencial de Coulomb. Diferentemente do potencial de Yukawa, podemos ver claramente que decresce muito lentamente, enquanto que o potencial de Yukawa decresce muito rapidamente (a depender da massa m). Por essa razão, dizemos que o potencial de Yukawa é um potencial de curto alcance, enquanto que o potencial de Coulomb não é. No gráfico que é apresentado ao lado, podemos ver como o potencial de Yukawa comporta-se, com a distância , para diferentes valores de .
Quebra espontânea de simetria é um processo pelo qual um sistema simétrico passa, de forma espontânea, para um estado não simétrico. Este tipo de processo, incomum na natureza física, é vital para a compreensão do modelo padrão das partículas fundamentais, que é um dos mais importantes ramos da física moderna.
Definição
Para que uma quebra espontânea de simetria ocorra, deve necessariamente haver um sistema no qual existam diversos estados subsequentes com iguais probabilidades de ocorrer. Este sistema, como um todo, então é tratado como um sistema simétrico. Entretanto apenas um dos estados subsequentes deve ocorrer e toda a probabilidade dos inúmeros estados diversos é reduzida a zero, já que não há mais simetria. Então, é dito que a simetria do sistema foi espontaneamente quebrada.
Definição formal
Quando uma teoria é dita simétrica com respeito à um grupo simétrico, mas afirma que um elemento deste grupo é distinto, então uma quebra espontânea de simetria ocorreu, ou seja, pela teoria, não é necessário que se identifique o elemento e sim apenas que haja um elemento distinto.
Importância no modelo padrão
Sem a quebra espontânea de simetria o modelo padrão prediz a existência de um determinado número de partículas. Entretanto, algumas destas partículas (os bosões W e Z, por exemplo) são preditos de não possuir massa, quando na realidade eles possuem massa. Esta era a maior falha do modelo até que o físico escocês Peter Higgs e outros propuseram, através do que ficou conhecido por mecanismo de Higgs, o uso da quebra espontânea de simetria para comportar massa nestas partículas. O mecanismo por sua vez prediz a existência de uma nova partícula, o bosão de Higgs. O bosão/bóson de Higgs foi detectado no LHC do CERN em Julho de 2012, com probabilidade maior que 5 sigmas de ser verdadeira tal identificação.
Uso na matemática
Na matemática o uso mais comum da quebra espontânea de simetria é pelo uso da Função de Lagrange, a qual essencialmente indica como um sistema irá se comportar por meio de termos potenciais
equação Graceli estatística tensorial quântica de campos 1 / / / G G [DR] = .= + G* = = [ ] ω , , / T] / c [ [x,t] ] = |
//////
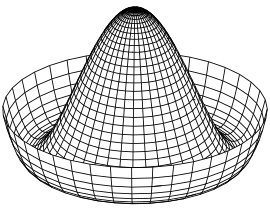
É neste termo potencial que a ação da quebra de simetria ocorre. Como demonstra o gráfico do chapéu mexicano
equação Graceli estatística tensorial quântica de campos 1 / / / G G [DR] = .= + G* = = [ ] ω , , / T] / c [ [x,t] ] = |
//////
Este termo potencial possui vários possíveis mínimos dados por
equação Graceli estatística tensorial quântica de campos 1 / / / G G [DR] = .= + G* = = [ ] ω , , / T] / c [ [x,t] ] = |
//////
para qualquer real no intervalo . Este sistema também possui um estado do vácuo quântico que corresponde ao , este estado possui um grupo unitário simétrico. Entretanto, uma vez que o sistema atinja um estado específico no vácuo (que corresponda a um valor para ) a simetria será espontaneamente quebrada.
Exemplos fora da Física
O fenômeno da quebra espontânea de simetria também é encontrado em Dinâmica de Tráfego de Veículos,[1] sistemas difusivos,[2] econômicos[3] e sociais.[4]
 /
/  /
/ 
 G
G 
















![{\displaystyle {\hat {\mathbf {v} }}={\frac {i}{\hbar }}\left[{\hat {H}},{\hat {\mathbf {r} }}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3970b2275f8d3808e3ebb6d143b6c6ee8db3912f)



![{\displaystyle [P,H]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9994e330ea898115e1554bafbac5bd18ef9815bf)























Comentários
Postar um comentário